Annie Chalon-Blanc

 La genèse de la catégorisation du réel selon Piaget et Inhelder : première partie 

Cet article fait suite à celui publié en 2023 : « Catégoriser le réel » où l’on distinguait les catégories naturelles (les schémas et les scripts) des catégories logiques (les classes). Il est peut-être utile de relire l’article de 2023 avant d’aborder la lecture de celui-ci.

Terminologie

Il est si fastidieux de se colleter avec la terminologie utile à comprendre les notions logiques et leurs traductions empiriques qu’un lecteur pourra préférer lire d’abord les points consacrés à l’expérimentation et à la genèse avant de revenir à la terminologie (cf., tableau récapitulatif à la fin du texte).  

Catégoriser le réel consiste à réduire la complexité de l’environnement physique et social en le découpant en schémas, en scripts ou en classes.

Toute genèse retrace le maximum possible d’étapes qui conduisent de l’origine des notions jusqu’à leur achèvement relatif à un moment donné, l’évolution étant en perpétuel devenir. 

Collection et classe

Dans les épreuves proposées aux enfants, le terme collection a deux significations : 1) il décrit le matériel utilisé, par exemple une collection d’images de chats pourra figurer la classe infinie des chats ; 2) il désigne les réalisations d’un sujet qui ne satisfait pas les critères empiriques de la construction des classes. On dit alors qu’il manie des collections.

Une « classe » se définit par sa compréhension et se délimite par son extension (Cf, ci-dessous). Une classe n’existe pas isolément mais appartient à un système d’emboitements hiérarchiques.

Relation de ressemblance et relation de convenance

La relation de ressemblance permet de réunir des objets qui se ressemblent : même espèce, même couleur, même forme etc. ; la relation de convenance préside au regroupement des éléments d'un schéma ou un script.    

Termes génériques et spécifiques

Le terme générique (B) désigne la classe emboitante, le terme spécifique (A) la sous-classe emboîtée la plus numériquement représentée, le terme spécifique (A’) la sous-classe la moins numériquement représentée appelée aussi la classe complémentaire de A sous B : (Ā). Par exemple, devant 10 animaux : 8 chats (4 noirs, 4 blancs) et 2 chiens (1 cocker, 1 caniche), on écrira (B) pour les animaux, (A) pour les 8 chats), (A’) pour les 2 chiens et (Ā) pour les animaux qui ne sont pas des chats, ici les 2 chiens (A’= Ā).

La disjonction et la réunion

Les classes A et A’ sont disjointes lorsqu’elles n’ont aucun élément commun, autrement dit, la classe vide (ø) est le produit de A X A’. Dans notre exemple, il n’existe pas d’animal qui soit à la fois un chat et un chien. La réunion (U) des deux classes contient tous leurs éléments : A U A’ = classe pleine (B), ici, les chats et les chiens sont tous les animaux représentés.

Appartenance partitive, appartenance inclusive et relation d’inclusion

L’appartenance partitive relie une partie d’un schéma ou d’un script à son schéma ou script d’ensemble.

L’appartenance inclusive (€) relie un élément à une ou aux classes auxquelles il peut appartenir. Ainsi, un chat appartient à la classe des chats, à celle des félins, des mammifères, des animaux etc.

L’inclusion est une relation entre classes, symbolisée par les signes : (être inclus : A < B ) ou > inclure (B > A).  La classe des chats est incluse dans celle des félins, incluse dans celle des mammifères, incluse dans celle des animaux, ... Tandis que la classe des animaux inclut la classe des mammifères qui inclut celle des félins, des chats, etc.

Extension et compréhension

L’extension d’une classe représente l’étendue des objets qui la constituent tandis que sa compréhension est la propriété générale commune à l’étendue de ces objets. Toujours, dans notre exemple, la compréhension « animaux » se rapporte à l’extension très restreinte de 8 chats et 2 chiens.

Méthodes de tri ascendante ou descendante

En réponse à la question : « Mets ensemble ce qui va bien ensemble », la méthode descendante consiste à réaliser d’emblée les collections minimales à partir de la sélection d’un élément dont une propriété a été isolée. Devant nos chats bicolores et nos chiens, un chat noir est pris, puis immédiatement tous les chats noirs ; ensuite un chat blanc suivi de tous les chats blancs, enfin tous les chats sont rapprochés les uns des autres et les deux chiens seront également rapprochés. En procédant ainsi, et sans tâtonner, toutes les collections minimales sont construites.

A contrario, la méthode ascendante consiste à isoler au coup par coup les éléments de la collection. Est pris le premier qui vient sous la main, puis celui qui suit ; si celui qui suit ressemble au premier, il est mis avec le premier mais s’il ne lui ressemble pas, il est mis à côté. Le suivant est pris ensuite et s’il ne ressemble ni au premier, ni au second, il est mis encore à côté. De proche en proche, sont ainsi réalisées toutes les collections minimales.

La dichotomie revient à rassembler en deux tas seulement toutes les collections minimales, et à fournir la compréhension de chacun des tas réalisés.

 Expérimentation

Devant une collection composée de 10 à 20 objets très hétérogènes (concrets ou imagés), le sujet doit d’abord la décrire, car les termes génériques et spécifiques doivent être connus de lui pour permettre le bon déroulement de l’épreuve. Les consignes sont ensuite présentées dans l’ordre suivant :

1°) « Mets ensemble tout ce qui va ensemble », cette première consigne permet de connaître le mode de catégorisation (naturel ou logique) et/ou d’enregistrer la méthode de classement (ascendante ou descendante) choisis par le sujet.

2°) Une fois les premiers tris réalisés, on demande de les dichotomiser : « Et maintenant, est-ce que tu pourrais faire deux tas ? », « Est-ce que c’est la seule façon de faire deux tas ? ».

En cas de réussite seulement, on poursuit : « Comment tu les appelles ? », puis devant deux collections (A et A’ incluses dans B) on évalue la construction de la relation d’inclusion en posant les questions ci-dessous :

* D’abord à l’aide des quantificateurs intensifs :  tous et quelques :

a) Est-ce que tous les B sont des A, par exemple : « Est-ce que tous les animaux sont des chats ? Pourquoi ? »

b) Est-ce que tous les A sont des B ? « Est-ce que tous les chats sont des animaux ? » sans jamais demander pourquoi.

c) Puis : Est-ce que tous les A sont quelques B ? Pourquoi ?  « Est-ce que tous les chats sont quelques animaux ? » Est-ce que c’est pareil de dire quelques B sont des A ou tous les A sont quelques B ?  « Est-ce que c’est pareil de dire quelques animaux sont des chats ou tous les chats sont quelques animaux ? »

* Ensuite vient la question de la quantification de l’inclusion :

Y a-t-il plus de A ou plus de B ? Pourquoi ? « Y a-t-il plus de chats ou plus d’animaux ? Pourquoi ? ».

Il convient de ne pas arrêter l’évaluation de la quantification de l’inclusion avec une seule représentation numérique des sous-classes, mais de la faire varier. Par exemple : 10 A et 2 A’, 4 A et 4 A’ ; éventuellement : 6 A seulement (A=B) ; cette variation est utile à éprouver la solidité des réussites et des échecs enregistrés.

La quantification de l’inclusion est considérée par Piaget et Inhelder comme le critère le plus fiable de la construction d’un système de classes (il sera affiné par Voelin,1976). Cette fiabilité est due au fait que les jeunes enfants, en réponse à la question : « Plus de B ou plus de A ? » préfèrent, à la comparaison inclusive, la comparaison disjonctive : « Il y a plus de A que de A’ (non cité) » tant elle est habituelle et « lisible » dans les données. Alors que la réponse : « Il y a plus de B que de A » est formelle.

Les critères les plus délaissés après Piaget, parce que trop saturés en facteurs linguistiques, sont ceux du maniement des quantificateurs intensifs. On peut le regretter, car ce sont d’excellents indicateurs du niveau intellectuel de l’enfant. Ajoutons même que, selon nous, la question : « Est-ce que c’est pareil de dire quelques B sont des A ou tous les A sont quelques B ?» mérite d’être posée à tous les enfants.

Population

Dans l’ouvrage publié en 1959 : La genèse des structures logiques élémentaires (G. S. L. E.), Piaget et Inhelder interrogent plus de 2000 enfants âgés de 3 à 12 /13 ans, ce qui est inhabituel chez ces auteurs qui préfèrent d’ordinaire enquêter avec la méthode clinique-critique (cf., article sur le blog) pour obtenir des protocoles de réponses très consistants. Ce qui implique de passer beaucoup de temps avec un sujet et restreint par conséquent la population expérimentale.

Mais, pour retracer la genèse des structures logiques élémentaires, Piaget et Inhelder font appel à de très nombreux expérimentateurs chevronnés afin de ne pas être taxés de bâtir leurs résultats et interprétations sur une dizaine de cas individuels. Ils classent leurs résultats en quatre stades que nous résumerons ici en quatre niveaux. 

Genèse

Niveau 1: Les collections figurales (âge approximatif : 3 ans à 4½-5 ans)

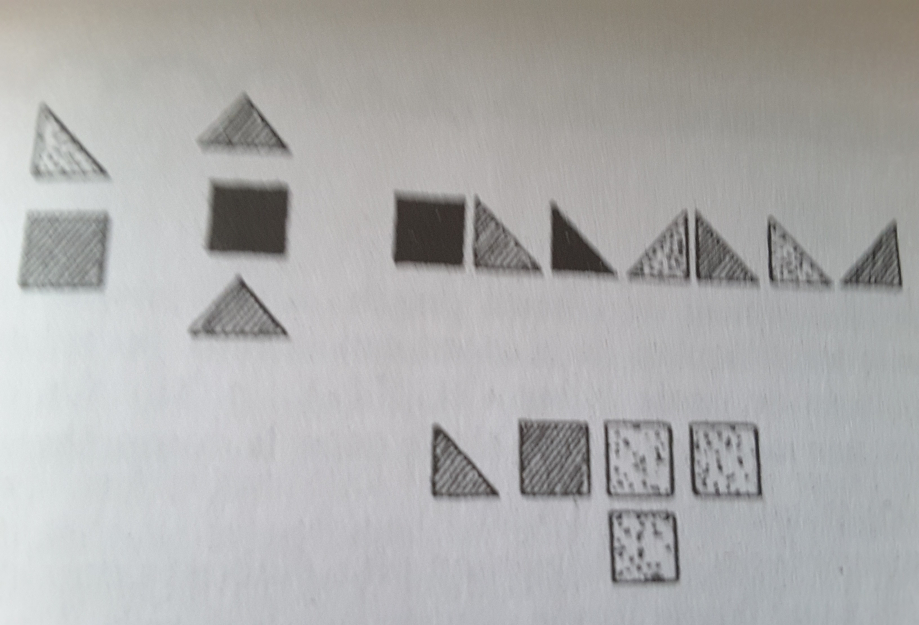
Évaluées à partir d’un matériel composé de couleurs différentes, fait en bois ou matière plastique, formé de cercles, carrés, triangles, anneaux et demi-anneaux, ces collections sont réparties en deux grandes catégories.

1. Les alignements (3 ans environ)

a)  Les alignements partiels. Le sujet ne cherche pas à regrouper tous les objets présentés et se contente d’en aligner quelques-uns. « Ces alignements partiels constituent les formes les plus simples d'assemblages » (G.S.L.E., p. 29).

Jos (3 ;1,) aligne d’abord six demi-cercles (deux bleus, deux jaunes, un rouge et un bleu). Puis elle met un triangle jaune sur un carré bleu, puis un carré rouge entre deux triangles bleus en rendant contigus les trois éléments de cette ligne. Elle construit ensuite un alignement de presque tous les carrés et les triangles (entrecroisés, sans relations de couleurs et se touchant). Puis aligne un triangle et trois carrés et décide en cours de route que c'est une maison : elle continue en ajoutant alors un carré en dessous des trois autres (Fig. 1).

(G.S.L.E., p. 30).

Fig. 1.

Jos, comme tous les sujets de cet âge, procède au coup par coup sans aucune anticipation ou rétroaction. Les relations de ressemblance sont établies de proche en proche et modifiées par simple contiguïté spatiale jusqu’à l’énonciation d’une convenance (maison).

b)  Les alignements continus (4 ans environ)

Chri (4 ;10) commence par aligner cinq rectangles bleus, dont le cinquième étant jaune, appelle quatre triangles jaunes suivis de deux demi-cercles jaunes. Ceux-ci provoquent alors le choix de cinq autres demi-cercles successifs de couleurs variées (Fig.2, G.S.L.E., p.31).                                                                                                            

Fig, 2.

  La généralisation de l’alignement à tous les éléments rencontrés aboutit à un alignement total, mais avec changement de critères en cours de réalisation. Le sujet commence à établir des ressemblances entre le premier élément choisi et le suivant puis entre le second et le suivant etc. Mais, ces éléments reliés par ressemblance de proche en proche ne sont pas encore assemblés en un ensemble total. « Quand les éléments satisfaisant au critère de départ (rectangle bleu) sont épuisés, le sujet continue l’alignement en cherchant une autre ressemblance, d’où le second critère (jaune). Cette apparition s’accompagne d’un oubli du premier critère parce que le début de l’alignement est trop éloigné dans le temps et dans l’espace. Le sujet se contente donc d’une ressemblance entre l’élément nouveau et celui qui le précède immédiatement » (G.S.L.E., p. 31). De sorte que, le sujet relie le dernier élément au précédent, sans que rien ne l'oblige à s'occuper du premier. Les ressemblances sont établies successivement. « Le sujet se borne donc à construire une succession spatiale et temporelle qui le rend inapte à figurer des systèmes de sous-classes et de classes totales, puisqu’une hiérarchie suppose un ensemble d’emboîtements et non pas une succession pure » (G.S.L.E., p. 31).

2. Les objets collectifs et complexes : les catégories naturelles (5 ans environ)

Lors de la réalisation des objets collectifs, les assemblages sont beaucoup plus élaborés que les précédents ; ils correspondent à une bonne forme donnée dès le départ. Des carrés qui se suivent, puis des petits carrés posés de manière symétrique de part et d’autre des grands carrés alignés, en haut et en bas de celui du milieu .

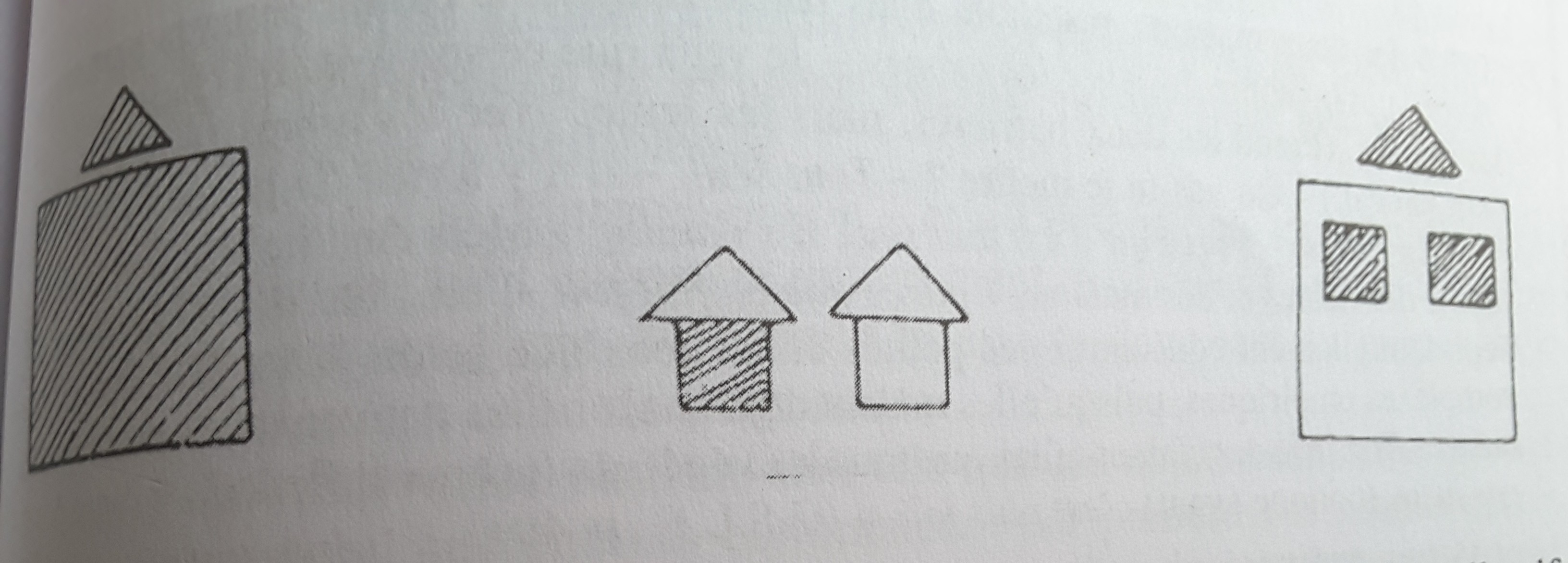
Après avoir commencé à réunir des carrés, ceux-ci font penser à une maison si bien qu’au lieu de continuer à prendre des carrés qui se ressemblent, l’enfant choisit des formes qui se conviennent : un triangle ou un petit carré pour constituer le toit ou la fenêtre d’une maison. C’est ainsi que la ressemblance de départ devient une convenance en cours de réalisation et que l’objet collectif se termine par un objet complexe que nous appelons maintenant un schéma (Fig. 3).

 Fig. 3.

Piaget et Inhelder vont insister, auprès des sujets, pour savoir si la relation de convenance, apparemment privilégiée, peut se transformer ou non en une relation de ressemblance. Ils leur présentent donc des feuilles de papier bien séparées afin qu’ils y classent les objets qu’ils viennent de réunir en objets complexes.

San (4;2) est face à de très nombreux objets (personnages, maisons, animaux, chars, sapins, barrières, fontaines, bébés et berceaux), tous susceptibles d'être réunis par ressemblance ou groupés par convenance selon le schéma d’un village. Le petit garçon pose sur une feuille trois arbres dont un sapin. « C'est pareil ? ‑ Oui les mêmes. ‑ (Il rajoute une maison) : ‑ C'est pareil, tout ça ? ‑ Des arbres et une maison. ‑ C'est la même chose ? – Oui - Que vas-tu mettre ? ‑ Deux messieurs et deux dames (rajoute ensuite deux bébés, un berceau et un char) - C'est la même chose ?  Je veux que ce soit la même chose. ‑ (Il reprend le char et le met sur une autre feuille avec des arbres, puis pose une maison avec les messieurs et les dames) ‑ Cette maison rose c'est la même chose que les dames ? ‑ (Il change la maison rose contre une rouge.) ‑ Pourquoi tu mets ça ? ‑ Il y a des hommes dans la maison ‑ Il faut mettre avec la même chose. ‑ Il met les deux maisons ensemble sur la feuille, puis il saisit la barrière. ‑ Avec quoi la mettre ? ‑ Avec les arbres. ‑ Je veux que ce soit avec les choses qui sont les mêmes – Il prend les deux barrières, les remet avec les arbres, puis attrape un petit cheval. ‑ Où vas-tu le mettre ? ‑ Tout seul. ‑ Il n'y a rien de pareil ? ‑ Le met avec les lapins - Parce qu'il est tout seul, il s'ennuie. » Met ensuite une fleur avec la feuille des dames et des maisons « parce que ça fait joli », etc. Après quoi San refuse des collections telles que tous les végétaux (arbres et fleurs) : « Non, c'est pas juste, (comme avant) c'est plus joli. »

(G.S.L.E., p. 49).

En dépit de l’insistance des expérimentateurs, le jeune San réunit les objets selon une relation de convenance et rejette la relation de ressemblance.  

Pour conclure sur les collections figurales, on retiendra que :

1)    – en réponse à une tâche de catégorisation, la pensée est statique : elle copie le réel dans la réalisation des collections ; elle est discontinue procédant au coup par coup par absence d’anticipation et de rétroaction. Aucune totalité n’est anticipée dans les alignements ; une totalité est réalisée dans la construction des objets collectifs ou complexes, mais sans anticipation puisque les relations de ressemblance s’y transforment en relations de convenance ;

2)    - les catégories naturelles précèdent les catégories logiques dans la genèse de la catégorisation. À l’exception des alignements, toute réalisation est un objet total. Or, seule une collection libérée de sa configuration spatiale permettra aux collections d’exister en tant que composées d’éléments discontinus et non pas en tant que formant un objet total (un schéma). 

Se pose dès lors la question de la filiation directe ou non des collections figurales avec les classes logiques. Peut-on considérer cette étape comme une étape nécessaire dans la construction des classes ? Jean Piaget a tenté de répondre à cette question. S’il est, à priori, paradoxal de considérer les collections figurales comme la première étape des classes logiques, puisque les classes demandent à être libérées complètement de leur assignation figurale alors que les collections figurales (sauf les alignements) y sont complètement assujetties ; les collections figurales sont néanmoins nécessaires dans la construction des classes. Elle le sont, car, ordre nécessaire oblige, elles suivent les alignements et viennent juste avant les collections non figurales, là où le logique commence à poindre et l’infralogique à s’éloigner. Et Piaget d’ajouter que les collections figurales sont délaissées par les enfants qui les considèrent, dès 9 ans, comme des solutions non pertinentes en réponse à une tâche classificatrice.

Cette affirmation d’une préférence précoce pour une réponse logique a suscité beaucoup de recherches (cf., bibliographie) qui ont mis en évidence la coexistence de ces deux modes de catégorisation tout au long de la vie, et qui ont, pour certaines, rejeté toute filiation franche entre les collections figurales et les classes (Rosch, 1976, 1983). La coexistence à vie des deux modes de catégorisation n’avait pas échappé à Jean Piaget qui mentionnait le délaissement des collections figurales en réponse à une tâche classificatrice et non pas leur disparition[1].

S’il est indéniable que les deux modes de catégorisation naturelle ou logique coexistent à vie, il est tout aussi indéniable d’affirmer que la catégorisation logique permet de classer le réel, soit de le distancier pour le comprendre. San (4 ;2), ci-dessus, n’a jamais vu réunis tous les végétaux ou tous les animaux : « c’est pas juste » dit-il à leur propos. Et pourtant, rien n’est plus justifié que ces réunions pour convertir le réel vu en un réel invisible mais organisé par tous de la même façon et intelligible par et pour tous.

Annie Chalon Blanc

Les niveaux 2 (les collections non figurales), 3 (les classes) et 4 (les classes complémentaires) seront exposés dans un prochain article.

Ci-dessous un tableau résumant les différences essentielles entre les schémas, les scripts et les classes

Références :

Piaget, J., Inhelder, B. (1959). La genèse des structures logiques élémentaires, Paris : Delachaux et Niestlé (pp. 9 - 52).

Piaget, J. (1969). Traité de psychologie expérimentale, vol. 7, Paris : P.U.F., 135-139.

Chalon-Blanc, A. (2005). Inventer, compter et classer, Paris : Armand Colin (pp.153-167).

Voelin, C. (1976). Deux expériences à propos de l'extension dans l'épreuve de quantification de l'inclusion, Revue suisse de psychologie pure et appliquée, 35, 269-284.

De la coexistence des deux modes de catégorisation, une sélection de lectures :

Bideaud, J., Houdé, O. (1989). Le développement des catégorisations : «capture» logique ou «capture» écologique des propriétés des objets? L’Année Psychologique, 89, 87-123.

Blaye, A., Bernard-Peyron, V., (1997). Catégorisations schématiques et taxonomiques : une étude développementale.

Blaye, A., Bernard-Peyron, V., Bonthoux, F. (2000). Au-delà des conduites de catégorisation : Le développement des représentations catégorielles entre cinq et neuf ans, Archives de Psychologie, 68, 59-82.

Houdé, O. (1992). Catégorisation et développement cognitif, Paris : P.U.F.

Lautrey, J (1998). La catégorisation après Piaget, Piaget après Piaget, Grenoble : La pensée sauvage, 93-102.

Lécuyer, R (2001). Rien n’est jamais acquis… Enfance, n°1, 35-65.

Rosch, E. (1976). Classifications d'objets du monde réel : origines et représentation dans la cognition, Bulletin de psychologie, N.S., La mémoire sémantique, 242-250.

Rosch, E. (1983). Prototype classification and logical classification: the two systems, in E.K. Scholnick (Ed).